实例类：

深度优先搜索关节点：

若有关节点，则将关节点删去后，图的连通性改变。

最长公共子序列：

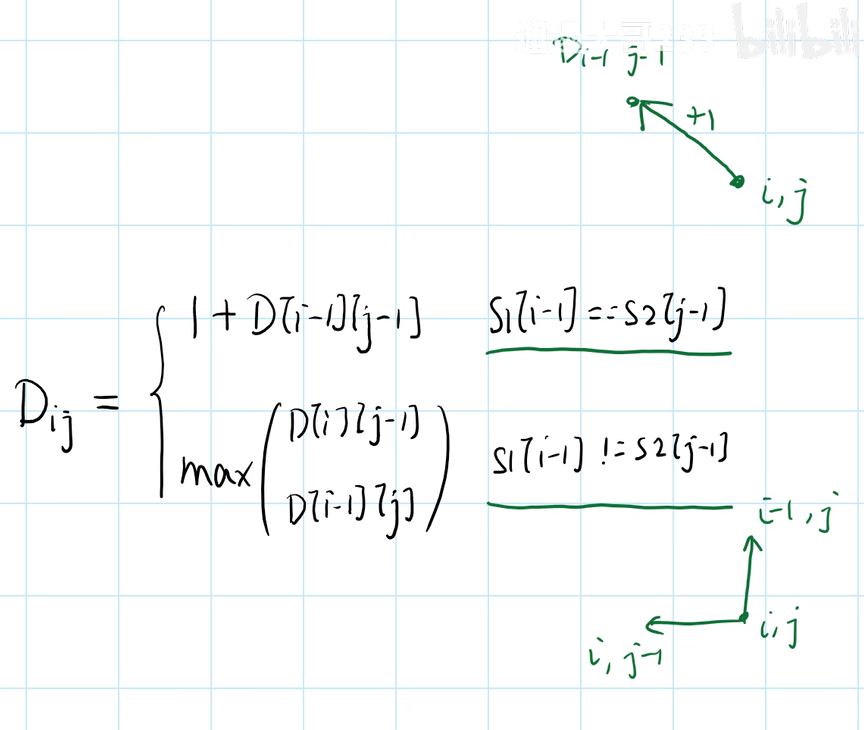
解释：若S1[i]==S2[j],则判断第S1[i-1]与S2[j-1]是否相同

若S1[i]!=S2[j],则选出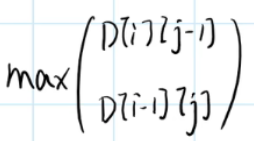

汉诺塔问题：

Hanoi（int n,int a,int b,int c）{    //把n个圆盘从a移到c
	if(n==1) move(n,a,b）//a上圆盘移到b
	else{
		Hanoi(n-1,a,c,b)
		move(n,a,c)
		Hanoi(n-1,b,a,c)
		}
}

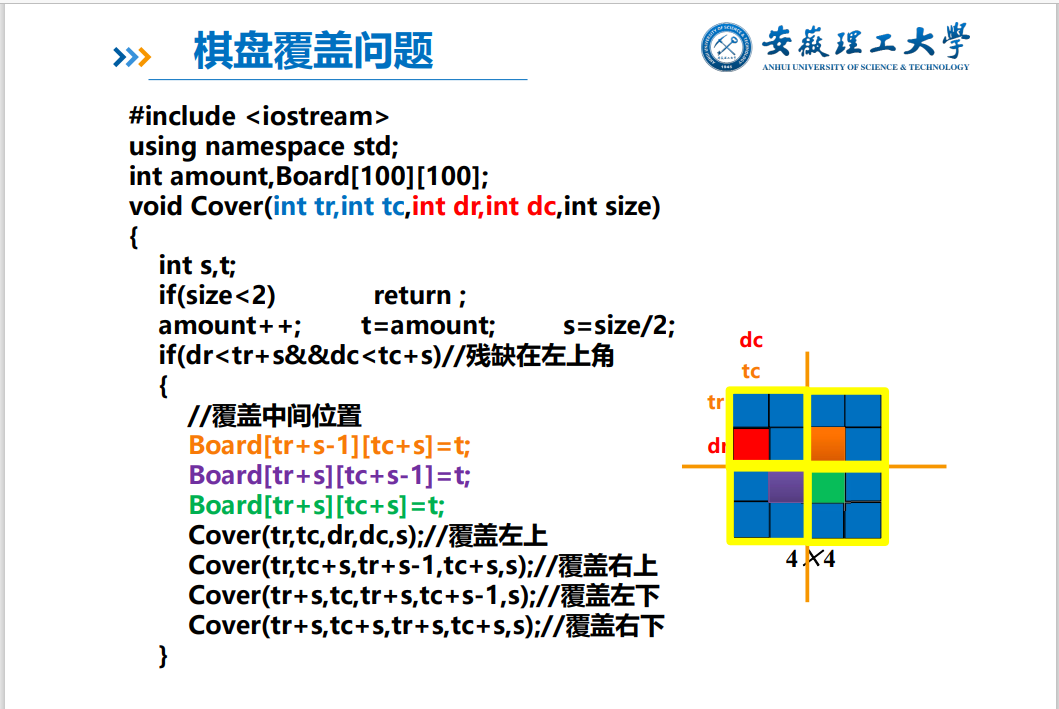
棋盘覆盖问题：

TR:该部分第一行第一列所在的行数

TC:该部分第一行第一列所在的列数

DR:残缺所在的行数

DC:残缺所在的列数

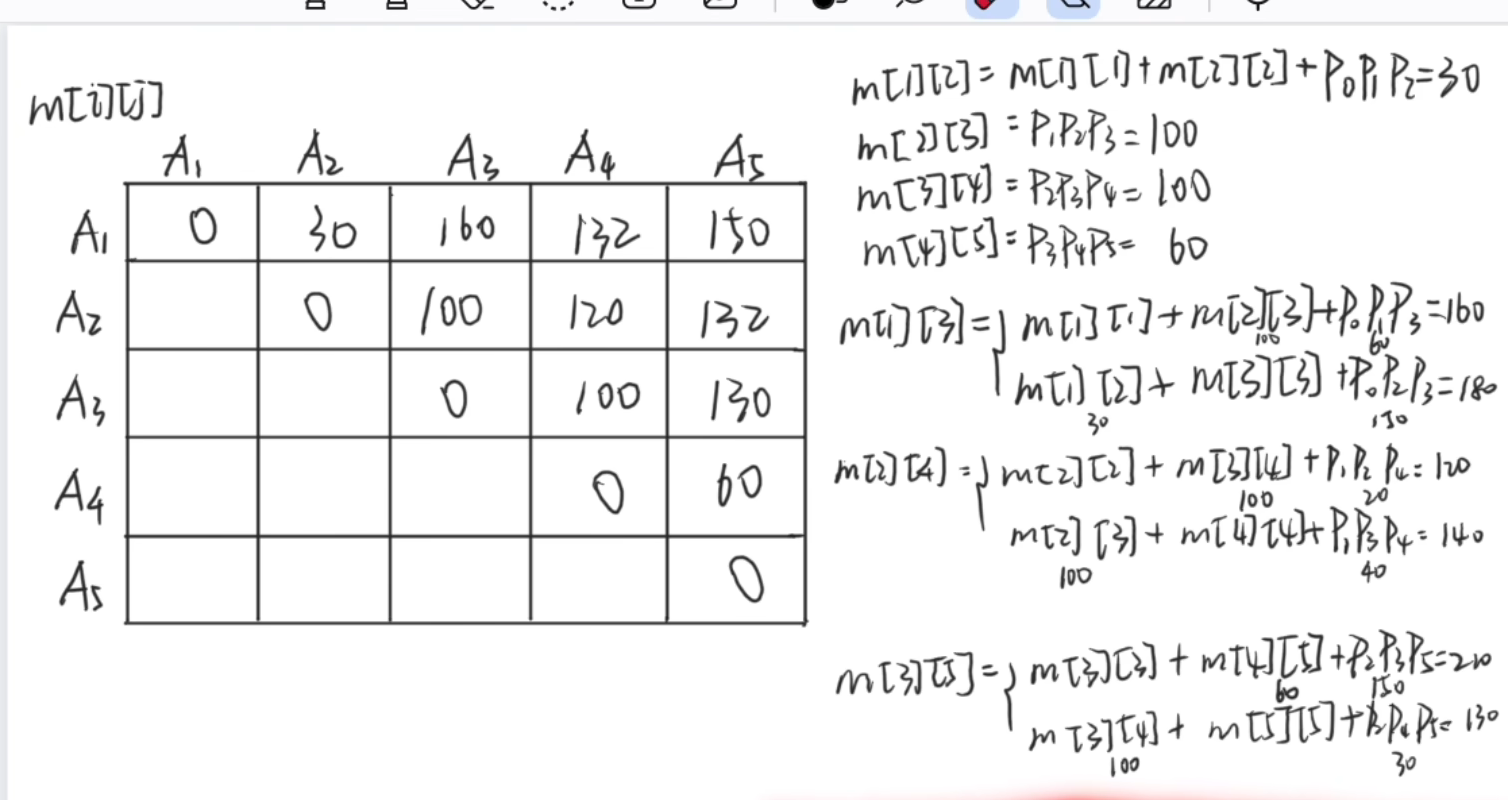
矩阵连乘：

所需最小数乘次数m[i][j]公式：

注！：以靠近0处优先计算

例：按如图右侧顺序计算

最大子段和：

【分治法：最大子段和】https://www.bilibili.com/video/BV183411z7EV?vd_source=8ba69158bd8924fc024f472b1ad2033c

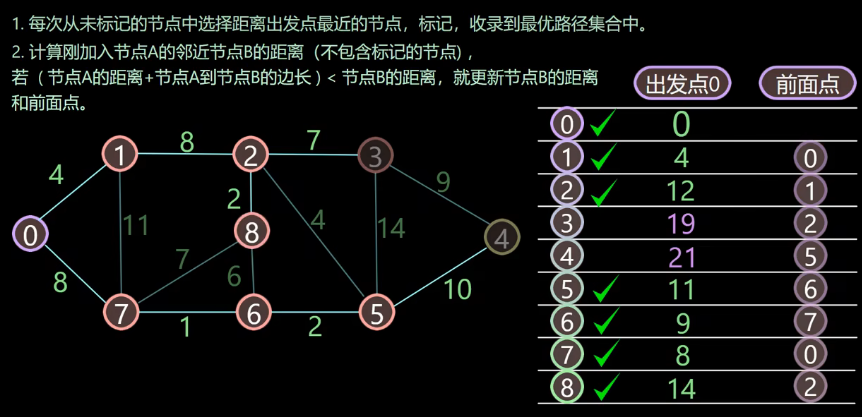
单源最短路径：

更新节点—>寻找距离出发节点最小节点 不断重复直至到达终点

哈弗曼编码贪心算法：

左大右小

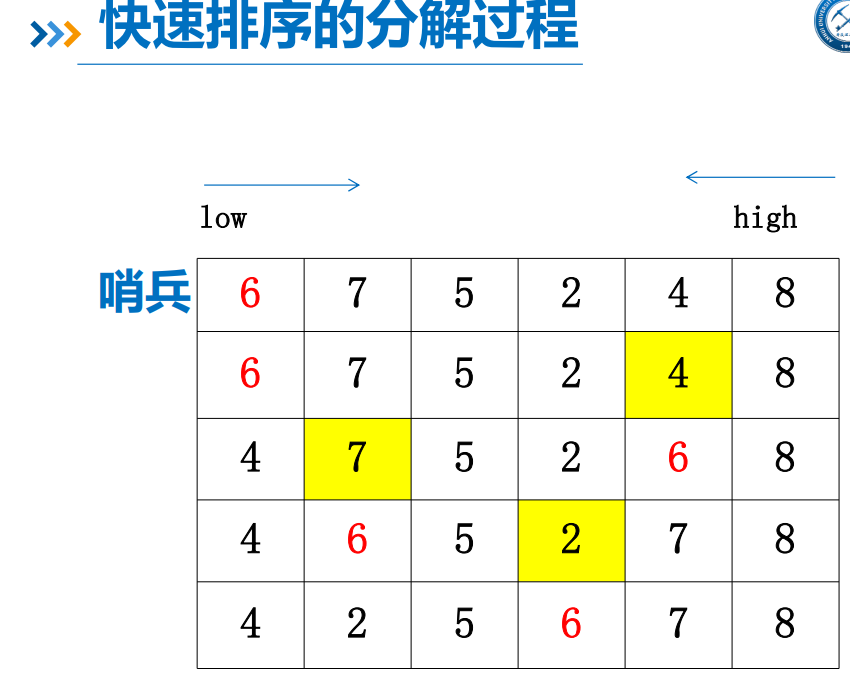
快速排序原理

数塔问题：

自下而上，完成动态规划过程存储

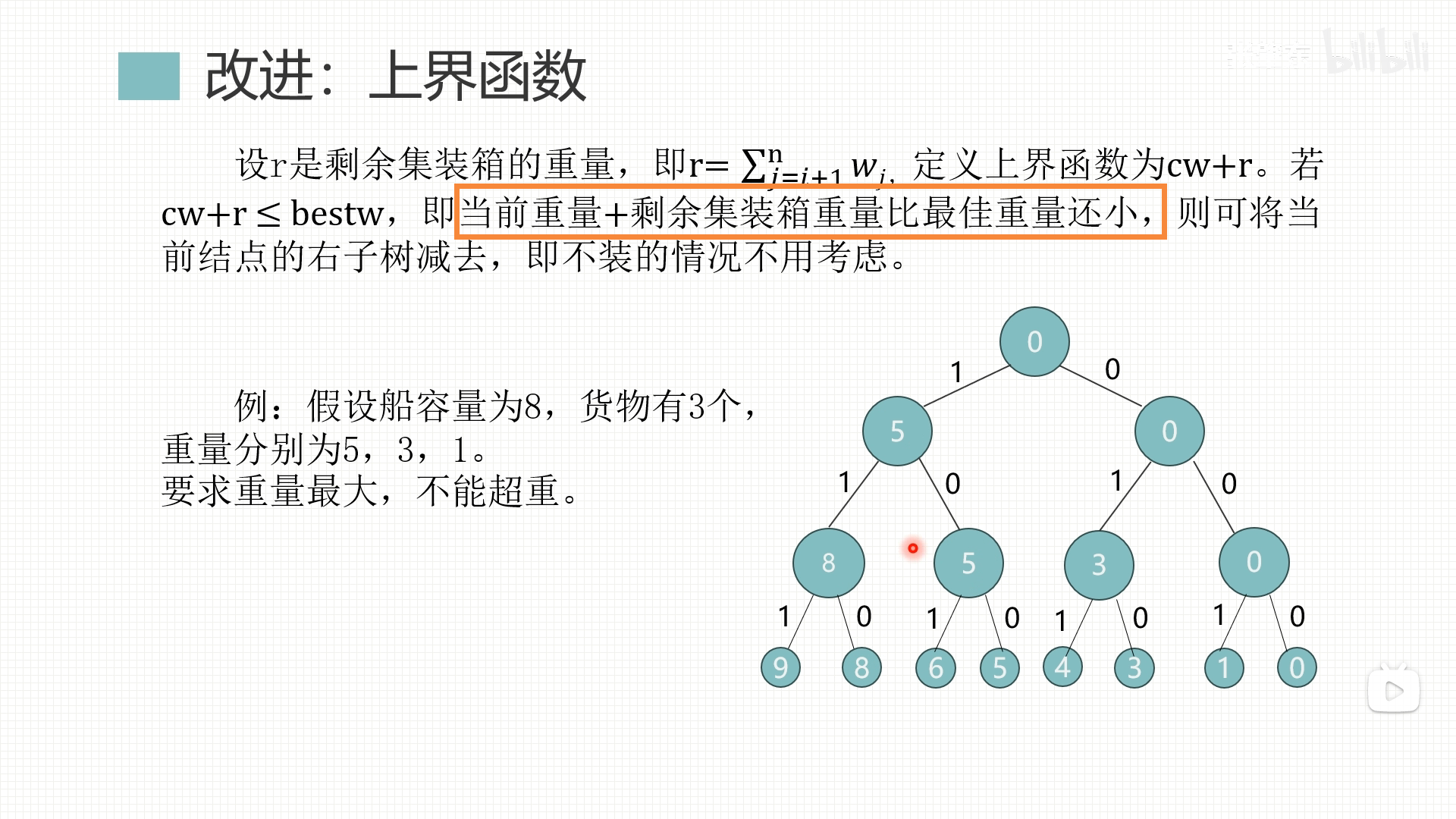
装载问题——回溯法

采用深度优先，并优化上界函数如图

若满足方框内条件，则剪枝

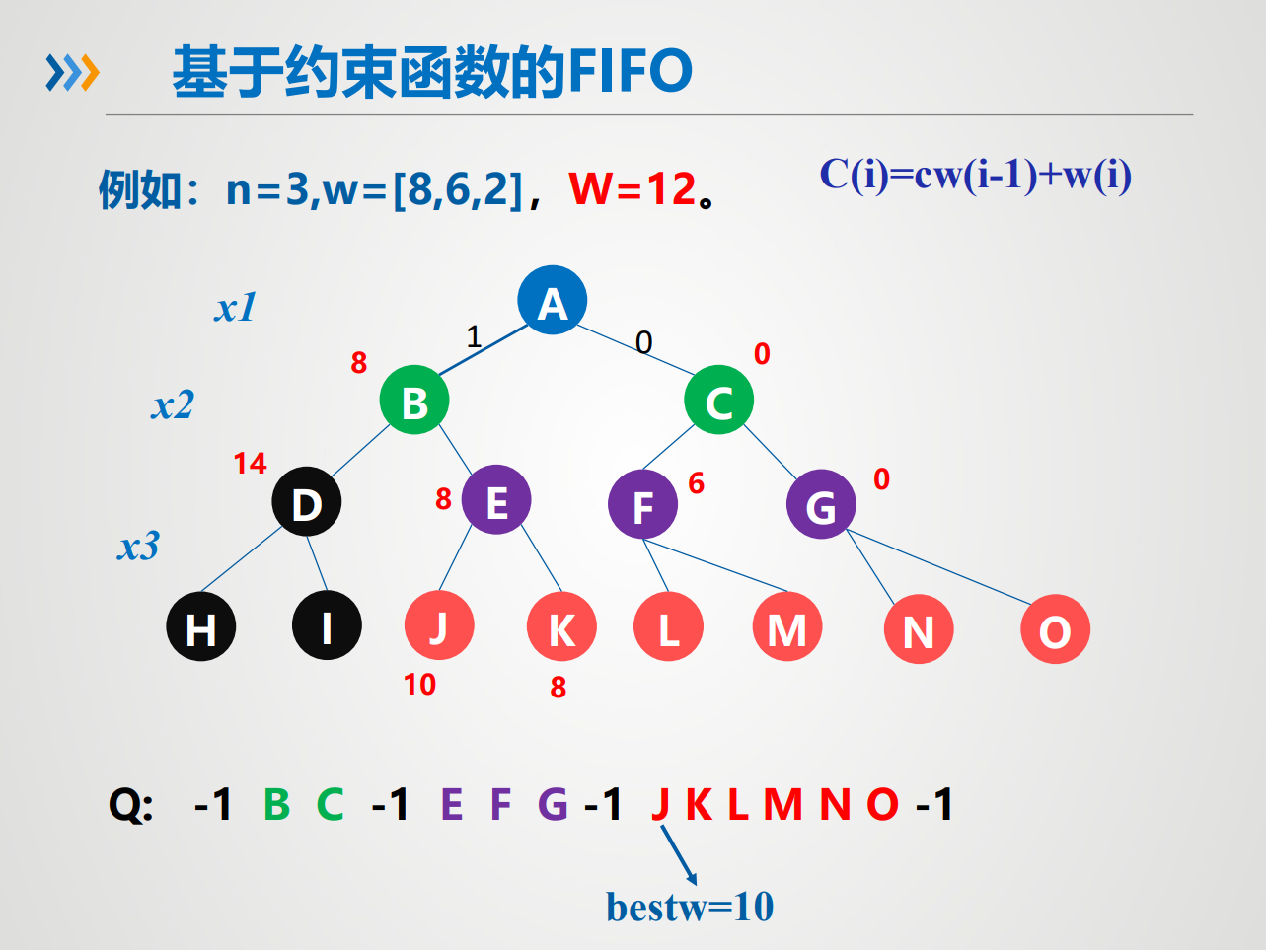
装载问题——分支限界法

采用广度优先，每当进入下一层时，队列压进-1

如图例：

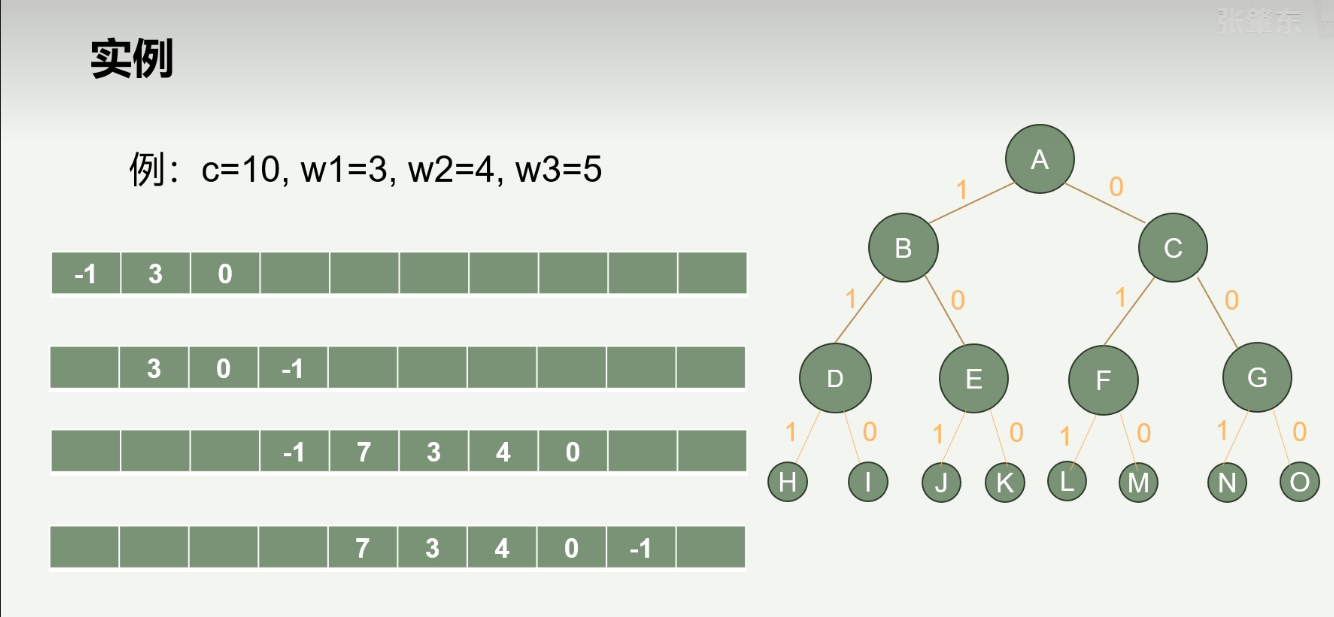
定义类：

算法定义：

面对具体问题，而想出的具体解决方法

算法三要素：

• 数据结构

• 操作

• 控制结构

算法性质：

1. 输入

2. 输出

3. 确定性

4. 有限性

5. 可行性

复杂度：

O：上界记号

Ω：下界记号

θ ：紧渐进界记号